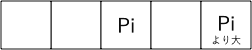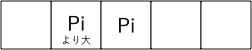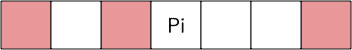ABC140E - Second Sum

問題概要

リンク

$1,...,N$からなる順列$P$がある。$1\leq L < R \leq N$となる$L,R$を選んだ時、$P_L,P_{L+1},...,P_R$の中で 2 番目に大きいものを$X_{L,R}$とする。

この時、$\sum_{L=1}^{N-1} \sum_{R=L+1}^{N} X_{L,R}$を求めよ。

制約

$2 \leq N \leq 10^5$

$1 \leq P_i \leq N$

$P_i \neq P_j (i \neq j)$

解法

問題が短くわかりやすいので一見簡単そうに見えるが、難しい。

$P_i=X_{L,R}$となる部分列の数

愚直にやると$L,R$の選び方で$O(N^2)$、各部分列の$X_{L,R}$を見つけるために$O(N)$なので、全体としては$O(N^3)$となってしまい間に合わない。

そこで、「ある部分列の$X_{L,R}$を求める」のではなく、「各$P_i$について、$P_i=X_{L,R}$となる部分列の数を数える」ことを考える。

$P_i$の値が$X_{L,R}$になっている、つまり 2 番目に大きくなっているような部分列とは、

のようなものや

のように$P_i$より大きいものを一つだけ含むような部分列である。

このような部分列の数を考えるために、以下のような、$P_i$よりも大きな値を赤色で表示した図を考える。$P_i=X_{L,R}$となる部分列とは、この図において、$P_i$と「赤色のものを 1 つだけ」含む部分列である。

そのような部分列の数は、$P_i$のすぐ左側か右側の赤を含んだ部分列をそれぞれ考え、そこから左右にどれだけ伸ばす余地があるかを調べることでカウントすることができる。

上の例で、左側の赤を含んだ最低限の部分列は以下のようになる。

この部分列から、赤を含まないように両端を伸ばすことを考えると、

• 左には 0,1
• 右には 0,1,2

だけ伸ばすパターンが考えられ、$2 \times 3=6$パターンの部分列が作れる。

右側の赤を含んだ部分列の場合も同様に

• 左には 0
• 右には 0

伸ばすパターンがあり、$1 \times 1=1$パターンの部分列が作れる。(つまり、これ以上伸ばす余地がない)

左右のパターンの合計は$1 + 6 = 7$となる。

$P_i=X_{L,R}$となる部分列の数を求める順番

$P_i$に対して上記のような計算をするためには、$P_i$よりも大きい数の出現位置が分かればよい。 よって、$P_i$の値が大きい順に部分列の数を求めていき、求めおわった$P_i$の出現位置を記録していけば効率的に計算することができる。出現位置の記録を二分ヒープなどで行うことで、$P_i$のすぐ左にある赤、そのすぐ左にある赤、$P_i$のすぐ右にある赤、そのすぐ右にある赤をそれぞれ$O({\rm log} N)$で求めることができるため、全体としても$O( N {\rm log} N)$で問題の解が求まる。