ABC139E - League

問題概要

リンク

N 人の選手が大会に参加する。各選手は 1 日 1 試合しか行えず、$i$番目の選手は$A_{i,1},A_{i,2},...,A_{i,N-1}$の順に試合を行う必要がある。試合の日程をこの条件を満たすように決めることは可能か。可能であれば全ての試合が完了するまでにかかる最小日数を求めよ。

制約

$3 \leq N \leq 1000$

$1 \leq A_{i,j} \leq N$

$A_{i,j} \neq i$

$A_{i,1},A_{i,2},...,A_{i,N}$は全て異なる。

解法

グラフとして考える

2 人の選手$i,j$の試合を行うことができる条件を考えてみる。

選手$i$は$A_{i,x} = j$となる$A_{i,1},...,A_{i,x-1}$までの試合($j$の選手と戦うまでの全ての試合)を終えている必要がある。$A_{i,x-1}$の試合を終えているためには$A_{i,x-2}$の試合が終わっている必要があるため、結局$A_{i,x-1}$が終わっていることだけを見ればよい。

選手$j$についても同様に、$A_{j,y} = i$となる$y$について、$A_{j,y-1}$の試合を終えている必要がある。

まとめると、

• $A_{i,x} = j$となる$x$について、$A_{i,x-1}$を終えている (x=0 なら$A_{i,x-1}$は存在しない)
• $A_{j,y} = i$となる$y$について、$A_{j,y-1}$を終えている (y=0 なら$A_{j,y-1}$は存在しない)

の 2 つを満たせば$i,j$の試合ができ、$A_{i,x}$と$A_{j,y}$を消化することができる。このように、任意の$i,j$の組の試合を行うためには、$0〜2$個のある組の試合が行われている必要がある。

この関係を図示してみると、$A = \left( \begin{array}{cccc} 2 & 3 & 4 \\ 1 & 4 & 3 \\ 4 & 2 & 1 \\ 3 & 2 & 1 \end{array} \right)$なら

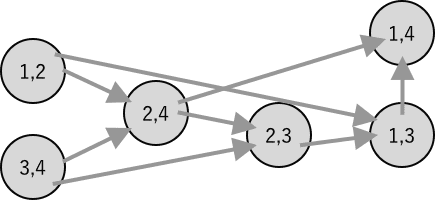
と、選手の組を頂点とした有向グラフとして表現できる。

このグラフでは各辺が$X$日から$X+1$日目の移動を表しているため、このグラフの最長パスの長さを求めることで、答えを求めることができる。グラフを構築するのに必要な計算量は、各選手の組(頂点)に対して張るべき辺は$O(1)$で分かるので、合わせて$O(N^2)$となる。

残る問題としては、

• 試合日程を組めないケースをどのように検出するか
• グラフの最長パスをどのように求めるか

がある。

日程を組めないケースの検出

入力例で日程を組めないケースとなっていた$A = \left( \begin{array}{cc} 2 & 3 \\ 3 & 1 \\ 1 & 2 \\ \end{array} \right)$についてグラフを作ってみる。

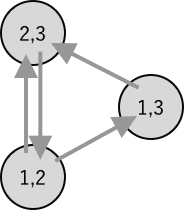
このように、明らかに日程が組めないことが分かる。全ての試合が他の試合に依存しているためである。 このようなグラフはトポロジカルソートが可能かどうかによって判定できる。

グラフの最長パス

まず、計算対象のグラフはトポロジカルソートができるので、DAGであることが保証される。DAG の最長パスは、以下のようにして求めることができる。

• 各頂点に対し、その頂点に訪問するまでにかかる最長距離$v[i]$を持っておく。最初は全ての$v[i]=0$。
• 各頂点をトポロジカル順序で見ていき、以下を行う。
• 現在見ている頂点と隣接する頂点$j$に対し、$v[j] = max(v[j],v[i]+1)$で更新する。

このアルゴリズムは全ての頂点に対してその頂点に隣接する辺を見るので、頂点数を$V$、辺数を$E$として$O(V+E)$となる。$V = N(N-1)/2$、$V$から出る辺は高々 2 つなので$O(N^2)$となる。

まとめ

選手の組みを頂点とし、先に終えておく必要がある選手の組みの試合を辺で表現することでグラフを構築する。グラフの最長パスが解となる。グラフの構築が$O(N^2)$、最長パスを求めるのが$O(N^2)$なので、全て合わせて$O(N^2)$である。