「estie プログラミングコンテスト2022(AHC014)」に参加した

October 04, 2022

「estie プログラミングコンテスト 2022(AHC014)」に参加しました。この記事では、自分の解法とどのように記録を伸ばしたのかを書いていきます。

問題概要

$N \times N$ 個の格子点を持つグリッド上に $M$ 個の点がある。プレイヤーは、下記の条件を満たすグリッド上に配置された 3 つの点 $p_1, p_2, p_3$ 及び点が配置されていない一つの格子点 $p_4$ を選び、グリッド上に点 $p_4$ と長方形を置くことを繰り返す。

条件 1: $p_1, p_2, p_3, p_4$ の順で線で結んだ時、並行、もしくは 45 度傾いた長方形をなす。
条件 2: 条件 1 で形成した長方形の外周上に、 $p_1, p_2, p_3, p_4$ 以外の点は存在しない。
条件 3: 条件 1 で形成した長方形は、グリッド上に他に存在する長方形と辺を共有しない。(点は OK)

点 $p_4$ を配置した時、同時に条件 1 で形成した長方形がグリッド上に配置される。このようにしてグリッド上に点を配置していくことを可能な限り繰り返すことができる。

グリッド上の格子点にはスコアが定められており、中心から遠い点ほどスコアが高い。配置した点によるスコアの総和が高くなるように操作を行うプログラムを作成せよ。

自分の解法

暫定順位 62 位、最終順位 67 位でした。

$\frac{m}{n \times n}$ の値に応じて場合分けを行いました。 $\frac{m}{n \times n} > 0.05$ のケースでは小さい長方形を優先する乱択、そうでない場合は完全ランダムの乱択を行いました。

$\frac{m}{n \times n} \leq 0.05$ のケースでの乱択

以下を 6 回行い、一番良いものを採用した。

全ての操作から次の手を選択し続け、次の手が無くなるまで盤面を更新し続けるという乱択を時間いっぱいまで繰り返す。
配置した点のうち最も重みが大きかったものを記録しておき、その点に到達するために必要な操作は次の試行にも引き継ぐ。

$\frac{m}{n \times n} > 0.05$ のケースでの乱択

以下を 6 回行い、一番良いものを採用した。

赤丸で囲んだ点からの並行な最小の正方形を使った下図のような操作のうち、上下のどちらか一方の組を奇操作、偶操作とする。
赤丸で囲んだ点からのナナメの最小の正方形を使った下図の操作のうち、上下のどちらか一方の組を奇操作、偶操作とする。(↑ とは独立に選択)
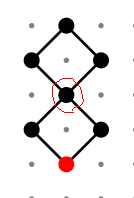
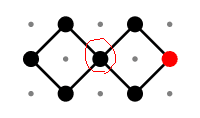
座標 $(x,y)$ において、 $(x+y) {\rm mod} 2 =0$ の点を奇数点、そうでないものを偶数点とする。偶数点を起点にした偶操作と、奇数点を起点にした奇操作を、偶奇が合う操作と呼ぶ。
初期盤面から、偶奇が合う操作が可能な場合はその操作の中から、そうでない場合は全ての操作のうち、長方形の面積が小さくなるものから次の手を選択し続け、次の手が無くなるまで盤面を更新し続けるという乱択を時間いっぱいまで繰り返す。
最小の長方形によって配置された点のうち、最大、または最小の $x$ 座標か $y$ 座標を持つ点を記録しておき、その名から最大 2 点を選ぶ。その 2 点に到達するために必要な操作は次の試行にも引き継ぐ。

コンテスト時の時系列

思い出しながら書いてある部分もあるので、正確でないかもしれません。

9/17(土)

用事があったので、問題文だけ確認した。操作回数については以下の操作を可能な限り好きなだけ繰り返すとなっていたので、うまいこと無限には操作を繰り返すことができないようになっているんだなあと思ったが、問題文を見ただけではよく分からず。

9/18(日)

ビジュアライザのマニュアルモードで遊んでみて、ようやく問題の意味をちゃんと理解できた。まずはパフォーマンス度外視で以下のようなコードを書いてみた。

今の盤面からできる操作のうち、最もスコアが高い点を配置できる操作を行う。
操作ができなくなったら終了。

深夜に上記の実装ができたので提出してみると、33308603点だった。時間は 78ms と結構かかっていた。

9/19(月)

方針は特に何も思いついていないが、今の実装が遅いので試行回数を稼げるようにひたすら高速化していくことにした。ナナメの線は座標を 45 度回転させてから計算するというややこしい実装にしていたのでその実装を消し、各点について 8 方向の最寄りの点を常に持っておく実装にした。これで 5 倍くらいの速さになった。また、ローカルツールに含まれていた問題例で、得点がいいシードと悪いシードを記録しておいた。

9/20(火)

次に可能な操作リストの計算を、新しい点を配置するたびに毎回行うようにしていたのを、「最新の操作に矛盾する操作を削除」「新しい点によって可能になった操作を追加」とすることで高速に更新するようにした。非常に面倒だったがなんとか実装し、相当速くなった。(大筋は解説放送で言っていた方法と同じもののはず)

共有されている seed0 で強いやつをみると、下記のように並行とナナメの最小長方形を使って点を増やしまくっている。(以下、「ヤグラを組む」と呼ぶことにする)

また、上記の検証のために問題例を作った時に、４隅に近い点は数点あるだけで絶大な威力を発揮することが分かった。(わずか 13 点で 220 万点！)

これらの実験から、まだ方針は全然考えついていないが、

ヤグラをどんどん組む
頑張って 4 隅近くに点を作る

のどちらかを成功させたいと考えた。

9/22(木)

ランダムな操作を選び続ける乱択と最小正方形を優先する乱択(ランダムなし)を作り、いくつかの問題で比べてみたところ、大体の問題例でランダムが勝利するが、seed8 のような初期の点が多い問題例では最小正方形優先が強いことが分かった。(ただし、ヤグラは全然組めていない)

9/24(土)

すでに置いてある点を一つ選んだ時、その点を置くのに必要な操作を抽出することを思いついたので、実装した。これを活用して、最もスコアのいい点に到達するための操作を行なった状態から探索を開始することで、最遠地点を更新していけるようにした。多様性を出すために、50%の確率で最もスコアのいい点に到達するための操作が行われた盤面、それ以外の場合は初期盤面から探索するようにした。この実装をランダムな操作を選び続ける乱択に追加してもなお、 seed8 では最小正方形優先の方が成績が良かった。一旦ランダムな操作を選び続ける乱択(+最遠への操作を保存)という方針で提出してみた。40680573点になった。

9/25(日)

なんの改善をしたかは覚えていないが、41089275点をとっていた。

9/27(火)

seed8 では最小正方形優先の方が成績が良かったので、初期盤面における可能操作の数が多い場合は最小正方形優先を使うように場合分けを追加した。44529587になった。

9/28(水)

最遠への操作を保存を入れてもそこまでいいスコアが出ないので、頑張って 4 隅近くに点を作る方針は難しそうだという結論に達し、最小正方形優先の方針をブラッシュアップしていこうと考えた。最小正方形優先は時間いっぱい使わず１回で終わりになっていたので、同率の操作がある場合はその中からランダムで選ぶようにして時間いっぱいまで回すようにした。こうするとちらほらヤグラが作られるようになり、提出してみると46221544になった。

9/29(木)

最小正方形優先にも最遠への操作保存を入れてみた。最遠点がヤグラの頂点とは限らないが、スコアは改善し、47220235になった。最小正方形優先の場合、操作を保存する頂点がヤグラの先端になっているのが望ましいと考え、最小正方形によって配置された、 $x$ または $y$ 座標が最小、または最大の点のうち重みが大きい上位 2 つの点を操作の抽出対象にしてみた。提出してみると48803395点。

ヤグラが組まれるには正方形が互い違いに設置される必要があり、この「互い違い」をうまく再現できないかと $x+y$ の偶奇で許容する操作を変える実装を追加してみた。これがうまくいき、ついに50031024に達した。

初期の点が少ないケースにも改善した最小正方形優先を適用してみたが、うまくヤグラを組む盤面にならず、ランダム操作+最遠点保存の方がスコアが高い。

現状、最小正方形優先が点の稼ぎ頭で 120 万~160 万という点を叩き出す一方、ランダム操作+最遠点保存は 80 万前後の点数しか取れてない状況になっているので、ランダム操作+最遠点保存を使っているケースを大きく改善できればかなりの得点アップが狙えそうだが、何も思いつかない。

9/30(金)

最小正方形優先の乱択でベストスコアを更新した時に、初期盤面から乱択を始めたのか最遠点に到達するための操作がある盤面から始めたのかを調べてみた。100%で最遠点に到達するための操作がある盤面からの開始だったので、初期盤面から乱択を開始するのをやめた。つまり、最終スコアも最初に発見した操作にずっと引き摺られてしまい seed によるスコアのブレが数十万とかなり大きかったので、4900ms をフルに使って 1 回回すのではなく、4920/6=820ms の時間を使って異なる seed で 6 回回すようにした。これで提出してみたところ、52128052点になった。土曜は用があったのだが、気づけば一睡もせず朝 7 時になっていた。

感想

自分の実装は初期の点の数が密な場合と疎な場合で場合分けを行い、疎な場合の動作はほとんど改善ができていなかったので、密なケースで稼ぎ、疎なケースをほとんど捨てるようなことになってしまいました。高順位の解法では焼きなましが使われてましたが、ある点を置くのに必要な操作を抽出することまでは思いつけていて土壌は整っていたにもかかわらず、これを使って焼きなましをするというのを思いつけなかったのが残念です。

ただ、密なケースではかなりうまくいき、最後まで手を止めることなく面白いように改善を続けていけたのでいつも以上にコンテストにのめり込んでいたと思います。めちゃくちゃ面白い問題でした。

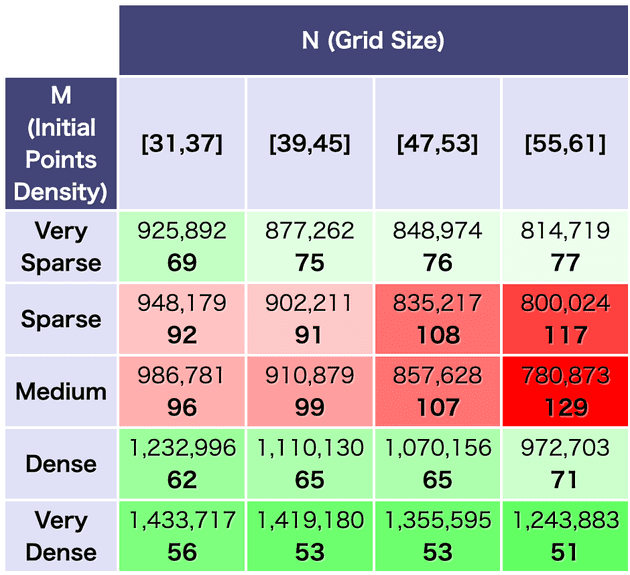
(「疎なケースをほとんど捨てる」が wleite さんが作ってくれた統計にもはっきりと現れていて、sparse、medium の行が真っ赤になっていた)