ABC111D(ARC103D) - Robot Arms

自力で解いたわけではないですが、かなり勉強になったので解答への筋道をまとめました。

問題概要

リンク

平面上の直交座標系の座標(0,0)に工場がある。さらに$N$個の点があり、それぞれ座標は($X_1$,$Y_1$),($X_2$,$Y_2$),…, ($X_N$,$Y_N$)である。

工場にロボットアームを導入し、$N$ 個の点全てに到達できるようにしたい。

ロボットアームは以下のような仕様である。

• $m$個の腕と$m+1$個の関節からなる。最初の関節の座標は工場がある(0,0)。
• 腕には L, R, U, D の 4 つのモードがあり、一つのモードを指定する。

• 腕を $1,2,...,m$、関節を $0,1,...,m$とした時、腕 $i$ は関節$i-1$と$i$をつないでいる。関節$i$の座標($x_i$,$y_i$)は、腕$i$の長さ$d_i$と指定されたモードにしたがって下記のように定まる。

  • ‘L’のとき、($x_{i-1} - d_i$,$y_{i-1}$)
  • ‘R’のとき、($x_{i-1} + d_i$,$y_{i-1}$)
  • ‘U’のとき、($x_{i-1}$,$y_{i-1} + d_i$)
  • ‘D’のとき、($x_{i-1}$,$y_{i-1} - d_i$)

ロボットアームの最後の関節が点$a$に一致している状態を$a$に到達しているという。

$N$個の点全てに到達できるロボットアームが存在するのであれば、そのロボットアームの各腕の長さと、$N$個の点それぞれに到達するためには各アームのモードをどう指定すればいいのかを出力せよ。ただし、腕の数は最大で 40 個である。

制約

• $1 \leq N \leq 1000$
• $-10^9 \leq X_i \leq 10^9$、$-10^9 \leq Y_i \leq 10^9$

解法

この問題のポイントは以下の３つ。

• そもそも、$N$個の点全てに到達できるようなロボットアームを作れるか
• ロボットアームの各腕の長さはどうすればいいか
• 各点へ到達するための腕のモードはどう決めるか

全ての点に到達できるか

訪れる点$a,b$について、点$a$に到達できるどのようなロボットアームを用意しても点$b$には到達できないということを確認できれば、不可能と判定することができる。

この判定を行うために、あるロボットアームについて、そのロボットアームで到達できる全ての点に共通する性質を考える。

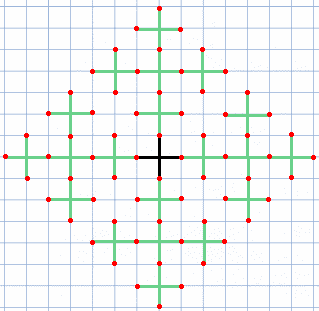
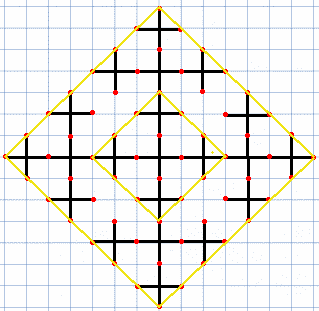
画像のように、ロボットアームが到達できる全ての点で、ロボットアームの長さの合計は等しい。 つまり、ロボットアームの腕を $1,2,...,m$ としたとき、ロボットアームが到達できる点($a_x$,$a_y$)で$a_x + a_y = \sum_{i=1}^m s * d_i$ ($s$は 1 もしくは-1)が成り立つ。

ところで、整数$a,b$について、$|a + b|$と$|a - b|$は奇遇が一致するため、ロボットアームが到達できる点($a_x$,$a_y$)全てで、$|a_x + a_y| \rm{mod} 2$の値は一致することになる。

よって、$N$ 個の点の$|a_x + a_y| \rm{mod} 2$を調べ、全て一致すれば可能、不一致なら不可能となる。

腕の長さはどうすればいいか

実は、問題の入力によらず、上記の条件を満たした$N$個の点全てにたどり着くことができる腕の長さの組み合わせが存在する。結論から述べると、$1,2,4,...,2^k$のように 2 の冪乗の長さの腕を用意することで、$|x+y|$が腕の長さの総合計以下となる点全てに到達できる。なぜこのようなことが言えるのかみていく。

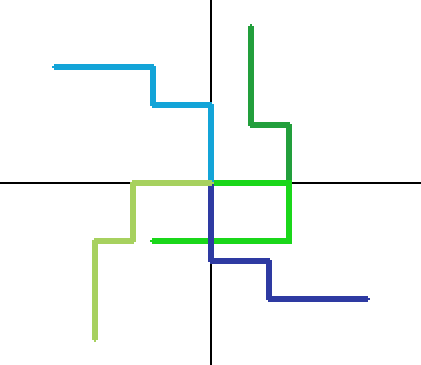
まずは、長さ 1 の腕が一つだけの場合を見てみる。$(0,1)$,$(1,0)$,$(0,-1)$,$(-1,0)$に到達することができる。

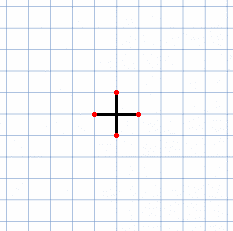
次に長さ 1,2 の腕がある場合を見てみる。

この場合、原点から上下左右に長さ 2 の腕を伸ばし、それぞれの点を基準に上記の「長さ 1 の腕が一つ」の状況を考えれば良い。$|x+y| \leq 1+2$で、$|x+y| {\rm mod } 2 = 1$の点全てに到達できていることが分かる。

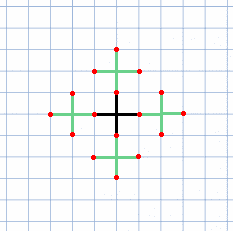
長さ 1,2,4 の腕がある場合も、$|x+y| \leq 1+2+4$で、$|x+y| {\rm mod } 2 = 1$の点全てに到達できていることが分かる。

同様に 1,2,4,..,$2^k$と腕を用意することで、$|x+y| \leq \sum^k_{i=1} 2^i$で、$|x+y| {\rm mod } 2 = 1$の点全てに到達することができる。全ての点が$|x+y| {\rm mod } 2 = 0$の場合は、長さ 1 の腕を一つ付け足せば良い。

制約から$|x+y| \leq 2 \times 10^9$なので、$1$から$2^{30}$までの長さの腕があれば全ての点に到達することができる。

腕のモードはどう決めるか

ここまでで、全ての点に到達できることの判定方法、腕の長さの決め方が分かった。あとはある点へ到達するための腕のモードをどのように決めるかを考える必要があるが、これは長い腕から順に考えていくことで解決する。

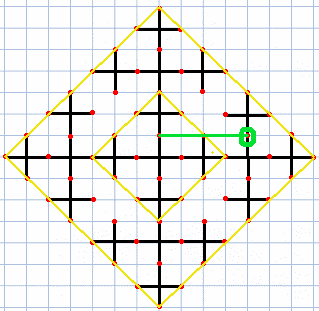
上図のように、腕$1,2$で到達できる点の集合は腕$1,2,4$で到達できる点の中に内包されており、これは一般的に成り立つ。これを利用すると、腕の長さ$1,2,...2^k$で到達できるエリアから、最も長い長さ$2^k$腕で腕$1,2,...,2^{k-1}$で到達できるエリアに動くことができれば長さ $2^k$ の腕のモードを固定できるという事になる。

つまり、中間到達点$p$を最初$(x,y)$とおき、最も長い腕を使って点$p$をまだ利用できる腕で到達できるエリアに次々移動させていけば全ての腕のモードが決まる。

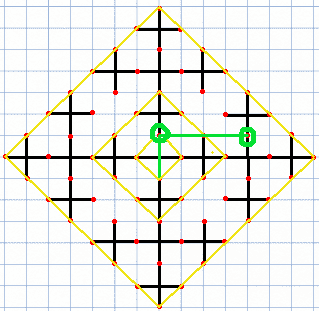
例として、点$(5,1)$に腕$1,2,4$の腕で到達する場合の各腕のモードの決め方を見てみる。

点$(5,1)$から長さ 4 の腕で腕$1,2$のエリアにいくには、長さ 4 の腕の腕で左方向に移動するしかない。これは移動後の座標$(0,1)$から長さ 4 の腕のモードを’R’にしたことに当たる。よって、長さ 4 の腕のモードは’R’と決まる。

続いて、点$(5,1)$から長さ 4 の腕で移動した点$(0,1)$から、長さ 2 の腕で腕$1$のエリアにいくには、長さ 2 の腕で下方向に移動するしかない。先ほどと同様に、長さ 2 の腕のモードは’U’と決まる。

最後に、$(0,-1)$から原点にいくには長さ 1 の腕を’D’のモードにすればよいので、全ての腕のモードが決定する。

腕の移動方向は、常に中間到達点$p = (x_p,y_p)$に対し、$|x_p + y_p|$が小さくなるように決めていけばよい。これは腕の数だけ操作を行うので$O(1)$である。

まとめと感想

結局、N 個の点全てに到達可能かを調べ、腕の長さ$1,2,...,2^{30}$の腕を使って、$N$個の各点について$O(1)$の操作で腕のモードを決めることで解を出力できるので、$O(N)$となる。

2 の冪乗の長さの腕を用意すれば全ての点に到達できるという発想にいくら時間があっても辿り着ける気がしなかったのでとても勉強になった。